Hough Transform: 곡선 인식과 기하학 패턴 활용 사례
Hough Transform이란 무엇인가?
Hough Transform(허프 변환)은 컴퓨터 비전과 이미지 처리 분야에서 직선이나 원, 타원 같은 기하학적 도형을 검출하는 데 사용되는 강력한 수학적 기법입니다. 1962년 Paul Hough에 의해 처음 고안되었으며, 그 이후로 다양한 형태의 변형(Generalized Hough Transform 등)을 통해 복잡한 형태의 물체 인식에도 활용되고 있습니다.
이미지 상의 선이나 곡선은 픽셀의 집합으로 표현되지만, 이 픽셀들을 하나의 구조적 형태로 인식하는 것은 고난도의 작업입니다. Hough Transform은 이러한 픽셀의 집합을 파라미터 공간(parameter space)으로 변환하여, 특정 형태의 도형을 효과적으로 검출할 수 있게 해줍니다.
Hough Transform의 작동 원리
1. 기본 원리: 직선 인식
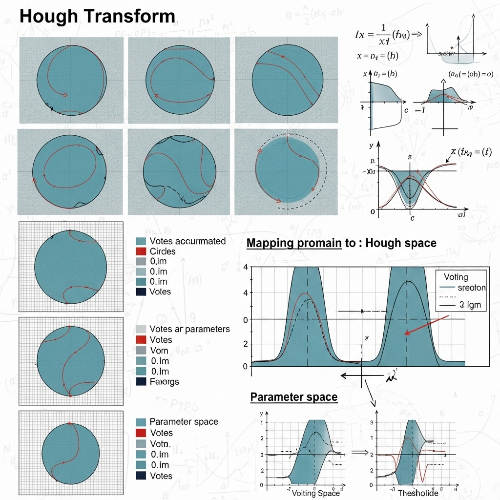
기본적인 Hough Transform은 2차원 평면 상의 직선을 찾는 데 사용됩니다. 한 점 (x,y)(x, y)를 기준으로 무수히 많은 직선을 표현할 수 있으며, 이들을 ρ=xcosθ+ysinθ\rho = x\cos\theta + y\sin\theta 형태의 방정식으로 파라미터화할 수 있습니다. 이때 ρ\rho는 원점에서 직선까지의 거리, θ\theta는 직선의 각도입니다.
여러 점들이 같은 (ρ,θ)(\rho, \theta) 값에 대응된다면, 이는 동일한 직선 위에 위치함을 의미하며, 결과적으로 이 직선이 이미지 내에서 존재함을 추정할 수 있습니다.
2. 누산기(accumulator) 공간 활용
허프 변환은 이미지의 각 엣지(Edge) 점에서 가능한 모든 θ\theta에 대해 ρ\rho를 계산하여 누산기 공간(accumulator array)에 투표합니다. 특정 (ρ,θ)(\rho, \theta)에 많은 점들이 투표했다면, 이는 직선으로 인식됩니다.
곡선과 원 인식으로의 확장
Hough Transform은 단순한 직선뿐 아니라, 원이나 타원과 같은 곡선 인식에도 응용될 수 있습니다. 예를 들어 원은 (x−a)2+(y−b)2=r2(x - a)^2 + (y - b)^2 = r^2로 표현되며, 중심 좌표 (a,b)(a, b)와 반지름 rr이라는 세 개의 파라미터를 갖습니다.
이를 통해 다음과 같은 고차원 누산기 공간에서 동작하게 됩니다:
- 원 검출: 중심과 반지름을 파라미터로 하는 3차원 누산기 사용
- 타원 검출: 중심, 축의 길이, 회전각 등 5차원 이상 확장 필요
이러한 복잡한 파라미터 공간에서도 Hough Transform은 효과적으로 형태를 찾아낼 수 있는 안정적인 알고리즘입니다.
실제 적용 사례
1. 차량 번호판 인식
자동차 번호판 인식 시스템(LPR: License Plate Recognition)은 번호판의 테두리를 인식하여 위치를 파악해야 합니다. 이때 Hough Transform은 직선을 검출하는 데 탁월한 성능을 보여, 번호판의 경계선 탐지에 사용됩니다.
2. 의료 영상 분석
MRI나 CT 이미지에서 혈관이나 골격 구조처럼 반복되는 곡선 형태를 인식해야 할 때, 허프 변환이 효과적으로 사용됩니다. 특히 혈관 내 삽입물(스텐트 등)의 형태 분석에 적합합니다.
3. 교통 표지판 인식
원형 또는 삼각형 도형을 기반으로 한 교통 표지판을 인식하는 데 Hough Transform이 자주 사용됩니다. 이미지에서 원형이나 다각형을 검출함으로써 사인(sign)을 정확하게 인식할 수 있습니다.
4. 산업용 결함 검사
제조업에서는 금속 표면이나 반도체 웨이퍼 상의 균열이나 불균일성을 탐지할 때 기하학적 패턴 분석이 필요합니다. Hough Transform은 반복적이고 규칙적인 패턴을 추출하는 데 매우 효과적입니다.
Hough Transform의 한계점과 보완 기술
1. 연산 복잡도
곡선 검출에서 필요한 파라미터 수가 많아질수록 누산기 공간의 차원이 증가합니다. 이는 메모리 사용량 및 연산량 증가로 이어지며, 실시간 처리에는 부담이 됩니다.
2. 노이즈에 민감
허프 변환은 엣지 검출 결과에 의존하므로, 노이즈가 많거나 엣지 검출이 불완전한 경우 정확도가 떨어질 수 있습니다. 이를 보완하기 위해 Gaussian smoothing 또는 Canny edge detection과 함께 사용합니다.
3. 픽셀 분해능의 영향
디지털 이미지는 이산화된 픽셀 기반이기 때문에, 정확한 파라미터 추정을 위해 해상도 조절이나 보간 처리가 필요할 수 있습니다.
발전 방향과 응용 가능성
1. GPU 기반 병렬 처리
최근에는 GPU를 활용하여 Hough Transform의 연산 속도를 획기적으로 개선하는 연구가 활발히 진행되고 있습니다. 병렬 처리 기반의 허프 변환은 자율주행 자동차나 드론 등 실시간 처리가 중요한 분야에서 활용도가 높습니다.
2. 딥러닝과의 융합
기존의 전통적인 Hough Transform은 규칙 기반 알고리즘이지만, 딥러닝의 전처리나 후처리 과정에서 보조 도구로 활용되기도 합니다. 예를 들어 CNN이 추출한 특징맵(feature map)에서 구조적 형태를 분석할 때 허프 변환이 유용할 수 있습니다.
3. 강화된 Robust Hough Transform
노이즈나 왜곡에 강한 허프 변환 변형(예: Probabilistic Hough Transform, Adaptive Hough Transform)들이 제안되고 있습니다. 이들은 보다 정확하고 빠른 구조 인식을 가능하게 합니다.
결론: Hough Transform의 현대적 의미
Hough Transform은 오랜 역사에도 불구하고 여전히 실용적인 도구로써 컴퓨터 비전 분야에서 널리 사용되고 있습니다. 특히 직선과 곡선과 같은 단순한 기하학 패턴을 빠르고 안정적으로 인식할 수 있는 기능은 자율주행, 의료, 보안, 제조 등 다양한 산업에서 핵심적인 역할을 수행하고 있습니다.
딥러닝과 같은 최신 기술과 결합되어 기존의 한계를 뛰어넘는 방향으로 발전하고 있으며, 앞으로도 정형 구조의 시각 인식 문제에 있어 중요한 수단으로 자리 잡을 것입니다.